Los números racionales

Como hemos dicho con anterioridad los números surgen de las necesidades humanas cotidianas, vimos la necesidad de los números enteros, ya que en el conjunto de los números naturales no se podía explicar por ejemplo el tema de las deudas. Veamos la siguiente situación: juan celebra su cumpleaños, y en el mismo hay 5 personas contándole a él, pedro que es el anfitrión de la fiesta decide partir el pastel en porciones iguales. ¿ Que porción del pastel le tocó a cada uno ?, pues en esa situación bastante cotidiana los números naturales y enteros no nos ayudan mucho, dado que el número que describe la cantidad no es un número entero , para empezar se debe notar que los números ¨enteros ¨ se llaman así porque son enteros, es decir, que no están divididos , y se tenía un pastel (1), es decir, que el número 1 , que es un número entero y natural describía la cantidad de pastel, había un solo, pero ahora que pedro lo partió (lo dividió) en partes iguales ya no se tiene 1. Entonces por logia ya no puede ser un numero entero, y es así como surgen las fracciones y a su vez los números racionales. La porción que a cada uno le tocó es un ¨ 1/5, es decir, 1 de 5 , o 1 dividido 5 ¨.

¿Qué son los números racionales?

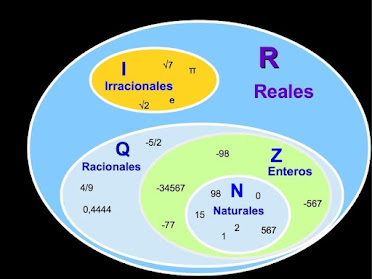
Los números racionales son un conjunto de números que incluyen todos los números enteros y fracciones. Un número racional se puede expresar como el cociente (división) de dos números enteros, donde el denominador no es igual a cero. En otras palabras, un número racional se puede representar como una fracción en la forma a/b, donde "a" y "b" son números enteros, y "b" no es igual a cero.

Los números racionales incluyen números enteros como -3, 0 y 5, así como fracciones como 1/2, -3/4 y 7/3. No obstante, es importante destacar que algunos números, como π (pi) y √2 (la raíz cuadrada de 2), no son números racionales, ya que no se pueden expresar como una fracción de dos enteros.

Representación de los números racionales

Los números racionales se representan típicamente en forma de fracción o decimal. Por ejemplo, el número racional 3/4 se representa como una fracción y como 0.75 en forma decimal. En una línea numérica, los números racionales se ubican en puntos intermedios entre los números enteros.

Propiedades de los números racionales

Los números racionales tienen varias propiedades importantes:

Cerradura bajo operaciones: Los números racionales son cerrados bajo las operaciones de suma, resta, multiplicación y división. Esto significa que la suma, resta, multiplicación o división de dos números racionales siempre produce otro número racional.

Orden: Los números racionales también están ordenados en una línea numérica. Esto permite comparar cualquier par de números racionales y determinar cuál es mayor, menor o igual.

Densidad: Entre cualquier par de números racionales, siempre se puede encontrar otro número racional. Esto es útil para la aproximación y la interpolación de valores en matemáticas y ciencias.

Teorema fundamental de la aritmética: Cada número racional se puede descomponer de manera única en un producto de números primos, similar a lo que ocurre con los números enteros.

Aplicaciones de los números racionales

Los números racionales se aplican en una variedad de campos, entre ellos:

Finanzas: Los números racionales se utilizan para calcular tasas de interés, realizar cálculos financieros y manejar datos económicos.

Ingeniería: Los números racionales son esenciales en la resolución de problemas de ingeniería, como el diseño de circuitos eléctricos y la optimización de sistemas.

Matemáticas puras: Los números racionales son una parte fundamental de la teoría de números y se utilizan en la resolución de ecuaciones y en la demostración de teoremas.

Física: Los números racionales se utilizan para describir relaciones entre magnitudes físicas, como la velocidad y la distancia en la física.

En resumen, los números racionales son una parte esencial de las matemáticas y tienen aplicaciones significativas en diversas disciplinas. Comprender sus propiedades y cómo se utilizan en la práctica es fundamental para desarrollar habilidades matemáticas y para aplicar conceptos matemáticos en la vida cotidiana y en campos profesionales.